100 m Sprint Prediction

Is there a limit to how fast a man can run ?Take a look at the world record times for the men's 100 m sprint from 1912 to 2002.

100 m Speed Demons		Date	Time
Donald Lippincott	USA	Sat 06 Jul 1912	10.6
Charles Paddock	USA	Sat 23 Apr 1921	10.4
Percy Williams	Can	Sat 09 Aug 1930	10.3
Jesse Owens	USA	Sat 20 Jun 1936	10.2
Willie Williams	USA	Fri 03 Aug 1956	10.1
Armin Hary	Germ	Tue 21 Jun 1960	10.0
Jim Hines	USA	Mon 14 Oct 1968	9.95
Calvin Smith	USA	Sun 03 Jul 1983	9.93
Carl Lewis	USA	Sat 24 Sep 1988	9.92
Leroy Burrell	USA	Fri 14 Jun 1991	9.90
Carl Lewis	USA	Sun 25 Aug 1991	9.86
Leroy Burrell	USA	Wed 06 Jul 1994	9.85
Donovan Bailey	Can	Sat 27 Jul 1996	9.84
Maurice Greene	USA	Wed 16 Jun 1999	9.79
Tim Montgomery	USA	Sat 14 Sep 2002	9.78

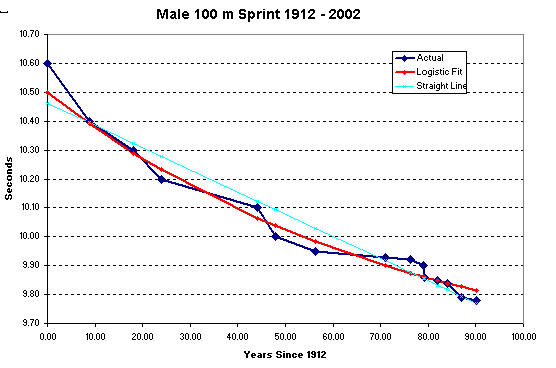
Table 1 - 100 m Sprint Records

The record is being improved in ever-decreasing changes. Montgomery has become world record holder by improving the mark by barely 1 part in 1000 - and you have to wonder whether the dimensions of the track and measurement of atheletes performance is really that accurate (particularly when the effect of wind swirls etc.,. is considered, notwithstanding rules etc.,. relating to wind assistance).

If the data is taken at face value, the following graph shows the reduction in speed improvements clearly...

100m
improvements

Figure 1 - History of the 100 m Sprint Record v Time

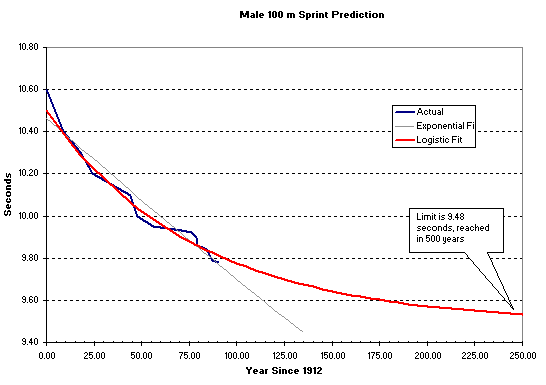
The dark blue line connects the individual record data points. A straight line fit to this is shown in the light blue line in Figure 1 above. This linear regression least-square error best-fit line over 90 years shows a slope of 7.7 millisecond fall per year. The correlation is 0.97, which is considered good for some applications (a best fit exponential gives virtually identical results).

Even if this straight line trend were correct, it would imply that in about 1300 years, the 100 m record would be run literally in no time flat (the record would be 0 seconds). This should be challenged.

The data over the last 90 years does not suggest the record will continue to fall as it did in the first 40 years to 1950. There are noticeable mismatches in the data, and the relationship over the first 20 years looks to have a different slope, to the middle 20 to 50 years and then the last 20 years.

A better correlation can be achieved by using a logistic equation to fit the data.

The logistic equation is very useful for modelling processes that are expected to reach a limit (see detailed discussion below). The correlation between the best least-square error logistic fit and the record data is 0.99 (1 is perfect fit). Although not a perfect match, it is a better statistical match than the straight line. The standard error of the fit is 0.031 - 50% of that for the least square error straight line fit (see table 6 below).

The logistic equation reaches a limit : 9.48 seconds. Shown below is the logistic model for the 250 years from 1912 to 2162.

250 year
logistic

Figure 2 - Future of the 100 m Sprint Record ?

It should be noted that in 1912, they didn't have running spikes, they didn't have starting blocks, and they didn't have all weather polyurethane tracks - all of which probably have contributed to a lowering of 100 m times. Hand-timing is often believed to have decreased recorded times (due to enthusiastic anticipation of the finish) - although some coaches claim professionally trained hand-timers were not susceptible to this. Quite simply, the contribution of these factors can not be ascertained - because we weren't there with the better technology.

So the best that can be done is to consider the overall result of the technological and biomechanical progress. Regardless of what the processes are that resulted in the improvement, each would also one day reach a limit. There is a limit to technological as well as biomechanical progress.

The Performance Enhancing Drugs (PEDs)

It wasn't clear when the above was written in 2002, but Montgomery's 9.78 was well ahead of time, and ultimately not credible. While Montgomery has not returned a positive drug test, according to press reports he testified to the US Anti-Doping Agency that he, along with a number of other prominent athletes (including baseball star Barry Bonds), used undetectable steroids and human growth hormone from BALCO, a laboratory near San Francisco.

On the 24 November 2008, Montgomery further admitted to taking testosterone and human growth hormone before the Sydney Games 4 x 100 metres relay (in Sep 2000), in which he helped claim the gold medal.

He was convicted of involvement in the BALCO steroid scandal and in Dec 2005 his results after 31 March 2001, including his world record, were stripped from the books when his final appeal to the Court of Arbitration for Sport failed.

This is what the logistic curve looks like if we strip Montgomery's record (click for a larger image)

Figure 3 - Updated History of the 100 m Sprint Record v Time- 2012

The Jun-99 logistic fit shows that Maurice Green's 99 record was 16 years ahead of the prediction from the curve. Montgomery's time was a 20 year leap forward. With a curve for Jun 1999, the long-run limit appeared to be 9.68 seconds. See Figure 4 below (click for larger image)...

Figure 4 - Long Range Predictions 1999 and 2009

Figure 4 also includes records to 2009 and shows a logistic fit for that.

100 Years - The Jamaicans

In the decade from 2002, along came the Jamaicans. The revised record table is now...

100 m Speed Demons		Date	WR Time
Donald Lippincott	United States	6-Jul-12	10.6
Charles Paddock	United States	23-Apr-21	10.4
Percy Williams	Canada	9-Aug-30	10.3
Jesse Owens	United States	20-Jun-36	10.2
Willie Williams	United States	3-Aug-56	10.1
Armin Hary	West Germany	21-Jun-60	10
Jim Hines	United States	4-Oct-68	9.95
Calvin Smith	United States	3-Jul-83	9.93
Carl Lewis	United States	24-Sep-88	9.92
Leroy Burrell	United States	14-Jun-91	9.9
Carl Lewis	United States	25-Aug-91	9.86
Leroy Burrell	United States	6-Jul-94	9.85
Donovan Bailey	Canada	27-Jul-96	9.84
Maurice Greene	United States	6-Jun-99	9.79
Asafa Powell	Jamaica	14-Jun-05	9.77
Asafa Powell	Jamaica	9-Sep-07	9.74
Usain Bolt	Jamaica	31-May-08	9.72
Usain Bolt	Jamaica	16-Aug-08	9.69
Usain Bolt	Jamaica	16-Aug-09	9.58

Table 2 - World Records as at 2012

Bolt's 9.69 almost beat the 1999 predicted limit, and his 9.58 smashed it to pieces.

As each new record is added, the updated logistic curve falls, but in each case, is still significantly above the new record time in 2012.

Figure 5 - Record by Record Curve Fits

Figures 4 and 5 show how remarkable these new records are. Montgomery's PED fuelled attempt took just 0.01 second off the record. Then came Asafa Powell, first shaving another 0.01, then another 0.03. Bolt then knocked 0.02, 0.03 then a whopping 0.11 from the record.

While the logistic fit equations are still a good approximation, it's clear that the "limit" predicted each time a new record arrives is falling. It falls from 9.6 seconds to 9.4. When Bolt's 2009 record is included, the limit falls to 8.96 seconds. And as can be seen from Figure 4, Bolt's 9.58 is well ahead of the curve - about 38 years before "its time" even when his data is included in the fit data.

The equation coefficients for the curves in Figure 5 are given in Table below. For comparative purposes, a least square error straight line has also been fitted to the data for several cases. For the older cases, the logistic fit is clearly superior, but it is only marginally better in 2009. The straight line fit would predict there is no limit - conceivably, one day a record of 1 second or less should be expected. The logistic fit is the simplest equation that can accommodate a limit, but it is obviously struggling to do this with the large performance improvements occurring before 2009.

	Logistic Fit					Line of Best Fit
*case*	*beta*	*delta*	P0	*Limit*	*Std Error of Fit*	*Slope*	*y intercept*	*Std Error of Fit*
6-Jun-99	0.188	0.0194	10.571	9.68	0.031	-0.0771	10.4631	0.060
14-Jun-05	0.167	0.0174	10.565	9.63	0.033
9-Sep-07	0.153	0.0160	10.564	9.58	0.035	-0.0763	10.4604	0.056
31-May-08	0.132	0.0139	10.557	9.50	0.037
16-Aug-08	0.101	0.0109	10.542	9.34	0.041
16-Aug-09	0.067	0.0074	10.533	8.97	0.055	-0.0795	10.4715	0.060

Table - 6 Best Fit Coefficients

The logistic fit coefficients (beta, delta, P0) shown in Table 6 can be used to estimate a date when the next world record should be expected - that is when the predicted 100m time is 0.01 seconds lower than at the record date. In each case, it's a long time away and for the last 10 years, performances have been well ahead of these predictions...

Date	New WR	Predicted Date
6-Jun-99	9.78	Nov-2024
31-May-08	9.71	Jun-2028
16-Aug-08	9.68	Nov-2027
16-Aug-09	9.57	Sep-2041

Table 7 - Predicted Date for New Record

The lack of a stable limit prediction as each new record is added over the last 10 years undermines its usefulness in making further predictions. Is there an explanation for what is going on that might give reason to believe the current predictions won't also fall short as time goes by ?

Explaining The Cliff Edge

Looking closer at the data, Usain Bolt improved the record by 0.11 second. That has never happened any other time in the 40 years since recording to 0.01 second accuracy started. Indeed, the previous best reduction was Maurice Greene's 1999 record which knocked 0.05 seconds off the record. Bolt's 2008 record had already taken 0.03 seconds off the record, making his contribution to the record reduction an astounding and unprecedented 0.14 seconds.

Bolt has driven the 100m sprint record over a cliff-edge.

And curiously, he's not recorded a time anything like it in the 3 years since 2009.
Since the 1980's, either the record holder or his contemporaries have run times within 0.05 seconds of the record in the following years. Nobody else has run within 0.1 seconds of his record, and even he hasn't got within 0.07 seconds

Here is a scatter diagram of sub 10 second performances since 1968 that shows how unusual it is (prior to London Olympics). Any runner who has an adverse doping incident in their history has been taken out (so no Yohan Blake or Justin Gatlin), as their performances aren't a credible reflection of human limits.

Figure 6 - All time best sub-10 second runs

Data on Bolts's 10m splits for his record run shows that Bolt holds his fastest 10 meter split of approximately 0.82 seconds for 40m. Other record holders can reach a 0.83 split, but hold it for only 10 or 20 m (see Usain Bolt 100m 10 meter Splits). That suggests that even for Bolt, there is a limit to the maximum speed a human can reach (0.82 s per 10 meters or approx 44 km/hr). He hasn't beaten that limit by much but has held it longer, and faded less than other runners.

Whatever training and development secrets have been found by Powell and Bolt have clearly not been discovered by their competitors. And could not be reproduced by Bolt or Powell either. Bolt's coach, Glen Mills, has been quoted as answering a "what's his secret" question from an investigative journalist thus:

"I hear you're from an investigative magazine," Mills says, looking as if he had just pronounced a curse. "Believe me, you won't find any secrets here."

While many commentators are happy to think of Bolt as a freakishly good athlete, others might wonder why its has taken so long for someone like him to emerge. Both are descendants from a gene pool exported by the Atlantic Slave Traders of the 16th to19th centuries to many destinations in South and North American, as well as other Caribbean nations. Yet it seems only the Jamaicans have been capable of turning the logistic model upside down.

For the London Olympics in July 2012, athletes blood samples will be kept for 8 years to allow retrospective testing. If any athlete has found a way to boost performance by pharmaceutical means that aren't presently detected, it might take 8 years to find out. If a pharmaceutical boost was delivered in (say) an athletes youth before they were subject to competition or out of competition testing, no one might ever find out.

Bolt ran the Olympic 100m final in 9.63 s with a 1.5 m tail-wind behind him (his 9.58 record had a 0.9 m tail-wind). Training pal Blake, who's tested positive for drugs, was second in 9.75 - fully 0.12 seconds slower. The USA's Justin Blake, having returned to the field after an 8 year ban for taking steroids, took the bronze medal with 9.79. Neither Bolt nor the drug takers could get anywhere near Bolt's 2009 record.

Post 1968 Data Fit

100m sprints were recorded to only 0.1 second increments prior to 1968. Interestingly, if the pre-1968 records are not eliminated, the logistic curve fit changes markedly.

Figure 7 - 100m Sprint Trend without pre 1968 records

It now has a convex shape to match the downward cascade in the 1968 to 2012 record. It is only marginally a better fit than a straight line (error of fit 0.048 v's 0.051).

The difficulty with a straight line fit is that it predicts that one day the 100m will be run in 0 seconds - and that's physically impossible. The convex logistic fit in Figure7 is just as troublesome - it approaches arbitrarily close to 0 seconds, and gets there quicker than a straight line fit. As shown in figure 8, by 2112, the record is predicted to be 8.2 seconds.

Figure 8 - 100m Sprint Trend without pre 1968 records (long view)

And in spite of being convex, Bolt's 2009 record is still well below the curve (i.e. ahead of expected time). Perhaps what this really shows is that choosing too short an historical record gives unsatisfactory nonsensical results, and still can't accommodate the Bolt cliff-face.

Annual Top 10 100m Runners

Some coaches have suggested that looking at the average times of the top ten runners might give a better representation of the trends. If there are one or two using undetected PED's etc.,., it might lessen the impact of their results on the trend. As at Aug 2012, the IAAF statistics page only publishes results back to 1996, so only that date forward is readily assessed.

For this exercise, the recorded times were adjusted to account for the effect of wind and altitude (using J Mureika's formula) in order to eliminate variability from those sources.

The data, logistic and straight line fits are shown in Figure 9. For each point, error bars showing one standard deviation above and below the averages are included as an indication of the spread of the annual data. Bolt's 2009 record is 9.63 after correction for wind and altitude, and that's 2.3 standard deviations below the mean (and off the bottom of this chart !).

Fig 9 Trend in Average of Annual Top 100m Athletes

The average data seems to fall as the Olympic years approach, then rises in the following year. This could be understandable, given the value athletes and their sponsors put on an Olympic medal.

As with fitting data to post-1968 data, the average of the top 10 also gives a logistic curve with an unbelievable convex shape that predicts a limit of almost zero. The logistic curve has an error of fit of 0.028, while the straight line is 0.029 - which probably is not a significant difference.

This limited average of top runners data can't identify a limit to 100m times.

Best Time Each Year

A longer data series can be formed by plotting the best 100m time recorded in each year, as shown in Fig 10. The least error fit of a logistic curve is also shown.

Fig 10 - Trend of Best 100m Each Year

While Bolt's 2008 and 2009 records are well below the logistic curve, it nicely bisects the last 6 points. The error in the logistic fit (0.060) is better than for the least-square error line (0.062).

Unfortunately, like all above cases taking data predominantly from after 1968, the logistic fit is heading south at a rapid rate. It's slope is -0.026 - over twice the resolution in timekeeping for world records. It gets even steeper approaching a slope of -0.154 seconds per year around 2063, as in Fig 11 - even more than Bolt's amazing contribution to lowering the world record.

And it makes an unbelievable prediction of a sub 1 second time (360 km/hr average speed) by 2100. The straight line fit has a much gentler slope - approximately 0.009 seconds per year, but it too gives unbelievable predictions of times below 1 second.

At this time, data from 1968 onwards can not identify any limit to 100m running times. The history of the world record times since 1912 shows a limit, but record runs in the last 10 years have each lowered the limit prediction.

it might take another decade of records, together with future and retrospective drug tests, before a trend that reveals a stable limit can be identified reliably. It took 3 years to discount Montgomery's record.

Carl Lewis has consistently questioned the performances of Jamaica's sprinters, refusing to join in the universal applause for Bolt after he raced to his first Olympic double at the Beijing Games in 2008.

"No one is accusing anyone," Lewis said in an interview shortly after the Beijing Games. "But don't live by a different rule and expect the same kind of respect ... I'm not saying they've done anything for certain. I don't know. But how dare anybody feel that there shouldn't be scrutiny, especially in our sport?

"The reality is that if I were running now, and had the performances I had in my past, I would expect (doping critics) to say something. I wouldn't even be offended at the question. So when people ask me about Bolt, I say he could be the greatest athlete of all-time.

"But for someone to run 10.03 one year and 9.69 the next, if you don't question that in a sport that has the reputation it has right now, you're a fool. Period."

Read more: http://www.smh.com.au/olympics/athletics-london-2012/ive-no-respect-for-him-bolt-reignites-lewis-feud-after-drug-slur-20120810-23yen.html#ixzz238TSOxVT

Usain Bolt took a further 0.1 seconds in the year after Carl Lewis's remarks. At the time of Lewis's remarks, Jamaica's anti-drug testing body JADCO was barely established. On the day Bolt created history by winning the 200 metres to complete the sprint double for the second Games in succession, Victor Conte - the convicted owner of the Bay Area Laboratory Co-operative (BALCO) that supplied drugs to the likes of Dwain Chambers and Marion Jones - had claimed it was easy for cheats to prosper at London 2012 and that 60% of athletes are using drugs. Conte supplied Tim Montgomery's with growth hormone and "the clear" - an undetectable steroid developed by BALCO.

When Bolt was questioned about Conte's comments, he finished off by unloading on Lewis - showing Lewis's 2008 remarks had gotten under his skin. Bolt's remarks prompted Olympics chief Sebastian Coe to respond

"I have no reason to believe that they are not testing out of competition. I think the IAAF... (in our) domestic and international testing arrangements have been very comfortable about how Jamaica and the Jamaican track and field federations are upholding those values and protocols,"

Head of JADCO Dr Wright also responded describing its regime as extremely good, involving testing in 40 weeks of the season and "unannounced" testing. That might leave 12 weeks of the season untested, and unannounced is not the same as random, and having no reason to believe isn't particularly strong if nobody is seeking a reason. When Jamaica's Shelley-Ann Fraser was convicted of drug use in 2010, WADA indicated it had inspected JADCO's program. Whilst finding it WADA compliant, its Director General David Howman said:

"In general it was a very positive report and there was nothing that made the agency non-compliant with the Wada Code.

"There were some suggestions for improvement around daily operational issues, such as sample collection, providing more out-of-competition tests and looking at potential conflicts of interest in several individuals who were closely involved in sports. And they are making strides in that direction."

http://www.guardian.co.uk/sport/2010/jul/10/shelly-ann-fraser-jamaica-anti-doping

So JADCO's program had flaws prior to 2010, and improving on those might be a factor in why Bolt and nobody else has matched his 2009 time.

Patrick Johnson

Australians got very interested in the 100 m Sprint in the week ending Sat 10th May 2003, when Patrick Johnson ran an Australian record of 9.93 secs (with 1.3 m/s wind assistance) on 6th May at Mito, Japan, and followed up on 10th with a 10.05 sec run (-0.3 m/s wind) in coming second to Tim Montgomery at Osaka, Japan.

What will it take for Montgomery to match his world record - and someone like Johnson from Torres-Strait Islander and Irish stock beat it ? See discussion below about wind effects for some clues (Jonas Mureika's wind and altitude correction calculator suggests Johnson's two May efforts were equivalent to corrected times of 10.02 (Mito) and 10.03 (Osaka)), but to really know the answer to who is the faster man you might have to look at 10 m splits for their races...

Trending Average Top Performances

Former Canadian track coach Charlie Francis suggested that averages of the top 10 and top 20 performances for each year since 1991(Charlie Francis discussion forum topic "9.48 in 500 years") might be a better indicator of performance trends.

Francis was Ben Johnson's coach at the time of his disqualification in the 1988 Seoul Olympics 100 m final, and was subsequently banned from coaching Canadian athletes. 1991 brought the arrival of Mondo Super X track, which might also have boosted performance (all-weather rubberised track with re-designed spikes that compress rather than dig into the track surface).

Looking at the average of the top performers shows that either performances are approaching a limit, or might have even gone through a slight up-turn. Is this the effect of better drug-testing ? As the analysis on the Comparison of 100 m Sprinting page suggests, the limit is very near and might have been reached. Low Sub-10 Sprints in 2003 presents a map of the sub-10 performances since 1987, and provides further evidence of a slow-down in performances.

Predictions of Limits

Other authors have predicted limits to performance. An ultimate limit of 9.37 sec is predicted by F. Péronnet and G. Thibault in``Mathematical analysis of running performance and world running records'', Journal of Applied Physiology, v.67, pp. 453-465 (1989) as cited in Jonas Mereika's paper "How Good Can We Get? Using mathematical models to predict the future of athletics" (published Athletics: Canada's National Track and Field / Running Magazine (April/May 1998)). Peronnet & Thibault's prediction of 9.73 s for Year 2000, however, has proven optimistic by about 0.06 secs; the record is not falling as quickly as they predicted, and the higher limit suggested above might be more accurate.

According to claims on the Charlie Francis discussion forums, Biomechanist Gideon B. Ariel Ph.D may have hypothesized in the late '70's that .: 9.60 would be the limit of the human body mechanically, that to exert the forces and limb velocities necessary to exceed this would crack bones and pull tendon from connection points.

No Limits to Performance ?

Some sports physiologists are more optimistic than this. For an intesting discussion prior to the Year 2000 Sydney Olympics, see W G Hopkins report in Sports Science Limits to Performance, and particularly the responses from Norway's Assoc Prof Stephen Seiler.

Seiler reports

I want to find out if we seem to be pushing the limits of human performance. Certainly people keep breaking world records. But are we getting to the point where training techniques are so good that it's only a matter of time before we top out -- before performance become essentially static, with only the occasional, once-every-generation super athlete able to set new records? Are we actually in a situation like that today with some sports?

What we found out when we looked at the 100 meter dash for men was that the average performance improvement was 0.01 second per year [~1% per decade] based on world championship and Olympic finals performances (average time of top 6 finalists) since 56 (corrected for wind and altitude). This improvement was linear and showed no sign of leveling off as of the end of the 20th century. Obviously, limits are being approached, but I think we can expect similar "steady" improvements for the next several decades. For example, Michael Johnson's "statistical outlier" 200 meter time in 1996 demonstrates that the potential for substantial improvements is still there (the women's data was much more complicated and I will leave it at that for the purpose of this discussion). The world record progression in many events is marked by these stochastic jumps, stabilization at a new level, new jump etc.

Seiler's fit of a straight line uses data only since 1956, and averages top performances not the peak performance (selecting performances at particular world-class events). Unfortunately, Seiler has not reported the goodness of fit in this discussion ( maybe he has in other publications). His method may be difficult, if not impossible, to extend back in time due to timing and recording inaccuracies. Other articles by Seiler at the site suggest he may have used film or videotape of performances to correct for hand-timing inaccuracies, and finding suitable archival material more than 50 years old could be impossible.

Seiler's methodologies are impressively complex. Does this complexity, however, go beyond what Occam's Razor might caution us to seek: "Pluralitas non est ponenda sine neccesitate" or "plurality should not be posited without necessity."

When giving explanatory reasons for something, don't posit more than is necessary (in, the vernacular, Keep It Simple Stupid) !

One should not increase, beyond what is necessary, the number of entities required to explain anything. From the discussion of Occam's Razor on Principia Cybernetica Web:

Though the principle may seem rather trivial, it is essential for model building because of what is known as the "underdetermination of theories by data". For a given set of observations or data, there is always an infinite number of possible models explaining those same data. This is because a model normally represents an infinite number of possible cases, of which the observed cases are only a finite subset. The non-observed cases are inferred by postulating general rules covering both actual and potential observations.

For example, through two data points in a diagram you can always draw a straight line, and induce that all further observations will lie on that line. However, you could also draw an infinite variety of the most complicated curves passing through those same two points, and these curves would fit the empirical data just as well. Only Occam's razor would in this case guide you in choosing the "straight" (i.e. linear) relation as best candidate model. A similar reasoning can be made for n data points lying in any kind of distribution.

...In mathematical modelling of systems, the principle can be made more concrete in the form of the principle of uncertainty maximization: from your data, induce that model which minimizes the number of additional assumptions.

If Seiler's model makes subjective assumptions about what is treated as a world class event for the purpose of constructing his statistics and how many performances to include (top 6, why not top 4, 8, 10 etc.,.), then it might not be minimizing the number of additional assumptions.

The discussion Hopkins reviewed includes viewpoints that there is no limit to performance. It raises such prospects as using gene therapy to insert the right muscle types into athletes, boosting their capacity. At what point ligaments, cartilage and perhaps even bones, give way and prevent a zero-second 100 m sprint is not clear - but with rewards for elite athletes sky-rocketing the temptation will obviously be there for some sportsmen to be willing guinea pigs.

Measuring Running Speed ?

Up until the 1968 Mexico Olympics, the 100 m sprint was hand-measured with stop-watches calibrated in tenths of seconds. So, as can be seen in Figure 1 above, the record fell in 0.1 second increments. Part of the inherent inaccuracy in this was the error due to the reaction time of the human timers. This could be between 0.1 and 0.2 seconds on starting and stopping, could vary between starting and stopping, and could vary compared to the runner's reaction to the gun. Measuring records in 0.1 second increments at least recognised the limited accuracy of the process.

For the 1968 Mexico Olympics, Jim Hines had several advantages: 0.01 second timing (allowing a new record just 0.05 seconds faster than the previous, and high altitude (equivalent to a 1.5 m/s wind assist, added to the 1.6 m/sec actual wind assistance). It's difficult to say how much of the improvement in his time may have been due simply to timing artefacts. Hines record stood for 15 years until Calvin Smith beat it in 1983 by just 0.02 seconds. That margin is so fine that if a light (eg. a LED) was flashed on for 0.02 seconds nobody would see it.

Some researchers have estimated the effect of altitude, and wind-assistance. J.R.Mereika's paper "A Matter of Time" (Published: Athletics: Canada's National Track and Field / Running Magazine (December 1999)) has estimated that the results could vary by as much as 0.18 second for the differing extremes of wind assistance (up to 2 m/sec) and altitude effects. The 0.18 seconds is nearly enough to cover all the improvement in the record for the last two decades!

The difference between no wind and 2 m/sec wind assistance could amount to around 0.1 seconds. Records that split this difference (by measuring to better than 0.1 sec resolution) could simply be measuring the varying contribution of wind. Tim Montgomery's 2002 record had the maximum legal wind assistance of 2 m/sec.

Don't think a 1 m/s wind can mess much with an 80 kg sprinter ? Think about this fact: a 390,000 kg 747 takes off with a 320 km/hr wind across its wings - that's about 90 m/s. Clearly, just being heavy or fast doesn't mean wind has no effect.

An average sprinter is 5000 times lighter than the 747, and a 5000 times lighter wind would be 0.02 m/s.

If sprinters were as aerodynamically efficient like a jumbo wing, they'd be literally flying at their peak speeds of close to 12 m/s (well over 0.02 m/s). Thanks to poorer aerodynamics (and lack of smooth laminar flow), they don't fly - but aerodynamic effects can still drag them back.

For more convincing evidence, watch TV footage showin how an approaching hurricane can blow grown men off their feet and into the air.

Beating the Gun or Running Fast

It is equally revealing to consider the effect of the start, and particularly the reaction time of the runners. The reaction time is the time is takes for the runner to respond to the start signal and begin leaving the starting blocks. (see Omega and Sport - Athletics for a good run-down of the sprint timing and start rules). Interestingly, it is considered that there is a limit to how fast a human can react to a start signal. As of 2002, if an athlete left the blocks sooner than 100 mSec after the start signal, he was deemed to have false-started.

The best athletes reaction times are usually in the range of 120 mSec to 160 mSec (see graphs). If you track individuals performances, there is usually a spread of 0.01 to 0.03 s in their reaction times. Until someone can consistently start in the same time (with less than 0.01 second variatin), it's fair to question what it means when events are timed in 0.01 second increments. At least some of the difference between world records and world class performances might have more to do with luck than something that can be honed by good training.

See Reaction Times and Sprint False Starts for more discussion of reaction times.

Peak Speed

Further insight can be gained by looking at the quickest 10 metre split attained by the runners - this shows the peak average speed reached. In 1988, with 1.1 m/sec wind assistance, Carl Lewis and the drug-fuelled Ben Johnson both hit a 0.83 sec split - or 12.08 m/sec ( = 43.37 km/hr). Lewis hit the same mark again in his Tokyo 91 world record run with 1.2 m/sec wind assistance. Maurice Greene's Athens 97 record, with a mere 0.2 m/sec wind assistance, could manage only a 0.85 split. In Seville 1999, Greene managed a 0.84 with a 0.2 m/sec wind assist, as did Dwain Chambers. Tim Montgomery's 2002 record run matched the 0.83 sec split, with 2m/sec wind assist (see Track And Field, Nov 2002). But over nearly 14 years, the peak speed has not been improved unless an allowance is made for wind assistance (making Greene's 99 performance perhaps the best).. This could be a strong signal that a limit has been reached.

Wind Assistance

When you get down to looking at one part in 100 changes to split times, it is wise to question what the wind-assistance figure represents. This has been researched by N.P Linthorne who reports(while with the University of Sydney School of Exercise and Sports Science):

Accuracy of Wind Readings

In the sprint events, races are timed to the nearest 0.01 seconds and the official wind reading is a 10 second measurement obtained from a single wind gauge placed next to the track. My wind assistance study indicated that if athletes are to be treated fairly when recognising world records the official wind reading must be accurate to ±0.2 m/s. It has long been suspected that the official wind reading does not always provide an accurate representation of the wind affecting the athlete as they run down the track.

A study of wind conditions at the Sydney Athletic Centre showed that the accuracy of the official wind reading is only about ±0.9 m/s. This is equivalent to an accuracy in race time of about 0.05 seconds. Therefore, the occasional injustice may arise in the recognition of world records. The accuracy of the official wind reading could be improved to the required level by using several wind gauges placed along both sides of the 100m straight. An instantaneous wind measurement would be taken as the runners passed by each wind gauge. However, this approach would greatly increase the cost and complexity of organising an event that meets the requirements for consideration of world records.

As Linthorne suggests, gusts and swirls at fortunate parts of the track could be affecting the results. The wind guage is required to have an accuracy of only 1 part in 10 (relative to the 2 m/sec limit being measured) - nothing like the 1 part in 1000 reported timing accuracy. Inaccuracy of 0.05 seconds could account for virtually all the difference between the last three world records (9.84 to 9.78 seconds).

Most of the recent improvement in the record has been due to improved reaction times (as shown for the Carl Lewis case above).. Is it really a record run, or just a record start ? If the improvement is purely due to luck or flukes in beating the gun, then what's the record worth ? What if it's just random wind gusts ?

The change in the starting rules may make gambling on fast-starts less likely and beating the records could be difficult without this advantage. If the 100 mSec false-start limit is reduced, and new records arise, will they be due to a genuine improvement in performance, or just good-luck in beating the gun ? How long will it be before anyone runs faster than Carl Lewis's 0.83 s split from 1988 ?

What effect will the April 2003 revelations of Carl Lewis and other American athletes positive drug tests have, if any ? Lewis was found to have tested positive to the stimulant ephedrine in the US trials in 1988. Is that how sprinters improve reaction times ?

The Comparing 100 m Sprinting - Wind & Altitude Correction page shows how correction for wind and altitude might affect rankings, and can also be useful in eliminating some of the variability in trends in average top performances.

Racehorse Limits

Thoroughbred Race Horses are the product of over 300 years of selective breeding. Today, racehorse records remain much the same as they were 100 years ago. As an example, Erica Goode reports (New York Times 8th May 2001, "Thoroughbreds Face Physical Limits to Improvement"):

The winning times for horses in classic races like the Kentucky Derby have remained surprisingly static. Secretariat's world-record-breaking Derby time of 1:59.25, for example, set in 1973, remains unsurpassed more than a quarter of a century later. Monarchos, this year's Derby winner, clocked the second-fastest winning time in history, running the race in 1:59.97, but still did not break Secretariat's record.

The reasons, scientists say, may have to do both with the unique physiology of the horse and the nature of the sport.

Horses are designed to run, their fleetness of foot having evolved over millions of years as a strategy of escape from predators. At one hour old, a foal is on its feet; at two hours, it is ready to go. And the horse's natural running ability has been nurtured and enhanced in thoroughbreds, which have been selectively bred for racing since the 17th century.

So while people require years of training and daily practice, thoroughbred racehorses enter the world much closer to their performance limits, said Dr. James Rooney, an emeritus professor at the University of Kentucky and an expert on equine biomechanics.

"The human is not, from the point of view of construction, a particularly good thing to start with and be an athlete," Dr. Rooney said. "But the horse is born to be an athlete. And the more they learn about horse physiology, the more people begin to realize that this animal has evolved to a certain point and you can't change it very much."

Lest you gather from this that Thoroughbreds have reached perfection, Loren Bolinger's 1998 article On the Manipulation of the Gene Pool What's Best for the Thoroughbred? -A Human Conceit, (once at "http://www.sunshow.com/pool.html"), gone by 2004)" raises a number of shortfalls in the history of thoroughbred breeding. This include a reluctance to incorporate female bloodlines until recent times, and disastrous destructive inbreeding. These mistakes and shortfalls lead to Loren's question on the wisdom of genetic manipulation:

The altruistic or otherwise tampering with the breed by latter-day well-meaning horsemen with that most noble of mankind's biological creations, the Thoroughbred horse, has largely been ill-advised, ill-conceived, and fortunately, historically relatively meaningless... Even with current advancements in molecular cyto-genetics, can we be sure we are as wise as Mother Nature? It would be a naive arrogance and a conceit to respond too quickly with an all-knowing yes. Be assured there are plenty of mysteries left to confound us. Are we so sure of ourselves or so smart to want to attempt to manipulate the gene pool of the Thoroughbred on any large scale? If such were the case, for what factors would we select - would we be wise enough to know beyond reasonable doubt the correctness of our decisions for the future of the breed?

It does not seem reasonable to expect human performance to improve forever and ever, when it's clear that human efforts - including selective breeding over hundreds of years - has not been able to achieve that for racehorses - does it ? Have we learned enough from the mistakes in thoroughbred selective breeding to not make even more disastrous mistakes with human athletic inbreeding ? Today's panacea, Genetic manipulation, may turn out to be hi-tech snake oil.

Interestingly, thoroughbreds continue to be raced while records no longer fall. Financial support for genetic manipulation of horses was so little that researchers have had great difficulty in funding the Horse Genome Project. The horse racing industry is not convinced of its potential benefits.

Racing is about competition - which is beating the other horse, not necessarily winning world records. Thoroughbread racing is also a lot about gambling, and that doesn't require record-breaking.

Eventually, the human 100 m sprint will get to that !

Mathematics of Logistic Equation

For there to be a performance limit, we need the Performance P(t) function to reach a limit at some future time - with no further change. The objective function is then:

dP/dt = 0                                       ...(1)

There clearly has to be a limit - even if it is the no-time-flat value of P_limit(t®¥) = 0.

We don't know what sort of function to use for dP/dt. Let's postulate that it might be some function of the current performance level (so that we can use current performance to predict future performance):

dP/dt = f(P) = 0                                ...(2)

The Taylor series expansion of any function f(P) gives:

dP/dt = bP + dP² + gP³ + ....                    ...(3)

Let's take to equation 3 with Occam's Razor. Using one term of the taylor series expansion for f(P) gives an exponentially increasing performance - and can't satisfy the objective (1) of reaching a limit (except for the trivial case of b = 0, which implies no change at all)

Taking the first two terms of the taylor series expansion is the simplest approximation to f(P) that will permit a non-trivial solution to (1).

dP/dt = bP + dP²                                       ...(4)

Solving (2) and (4) gives

 0      = P_limit ( b + dP_limit )

hence

b + dP_limit= 0
 
 P_limit = - b /d                       ...(5a)

( 
Since 

 P_limit >= 0
 
 we would expect that b  >= 0 and d <= 0  in equation (9).
 )

The solution to the differential equation in (4) is given is

log eqn

Summary: The logistic equation is the simplest mathematical model that captures a process of change that reaches a limit.

Applications of Logistic Equation

The Solver feature of Microsoft Excel can be used to to fit data to the solution to (4). Instructions for this can be found on further discussion of the Logistic Equation, which includes application to fitting Australia's population growth and links to applications to airport growth modelling. Updated Airport Growth for Sydney Airports shows how well the logistic model has predicted growth at Sydney's KSA airport (in comparison with exponential estimates and experts' guesses).

An in depth discussion of modelling the growth of foot and mouth disease with a logistic equation can be found here. For application of logistic equations to the 2003 SARS epidemics in Hong Kong, Singapore and Canada see Forecasting SARS.

Kevin Duffy's Home Page

90 Years of Records